Goal
Explore a bespoke neural network model sculpted for the iconic MNIST digit recognition challenge. This PyTorch-based endeavor magnifies the details of convolutional layers, pooling operations, and gradient descent techniques. The architecture, tuned and tested exclusively on the MNIST dataset, embodies the holistic learning journey from data preprocessing to pixel-perfect digit classifications.
Import Packages
import os
if ('google' in str(get_ipython())):
from google.colab import drive
drive.mount('ME')
#predir='/content/ME/My Drive/'
predir='ME/My Drive/'
else:
predir = os.path.join('Users','amit','Google Drive')
if os.path.isdir(os.path.join(predir,'My Drive')):
predir=os.path.join(predir,'My Drive')
import torch
import numpy as np
# Torch functions
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# Utility to track progress of a routine.
#from tqdm import tqdm
from tqdm.notebook import trange, tqdm
# Folder with course data
datadir=predir
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
Drive already mounted at ME; to attempt to forcibly remount, call drive.mount("ME", force_remount=True).
Get Mnist data and split into train validation and test
def get_mnist():
data=np.float64(np.load(datadir+'MNIST_data.npy'))
labels=np.float32(np.load(datadir+'MNIST_labels.npy'))
print(data.shape)
data=np.float32(data)/255.
train_dat=data[0:55000].reshape((-1,1,28,28))
train_labels=np.int32(labels[0:55000])
val_dat=data[55000:60000].reshape((-1,1,28,28))
val_labels=np.int32(labels[55000:60000])
test_dat=data[60000:70000].reshape((-1,1,28,28))
test_labels=np.int32(labels[60000:70000])
return (train_dat, train_labels), (val_dat, val_labels), (test_dat, test_labels)
Get the data
def get_data(data_set):
if (data_set=="mnist"):
return(get_mnist())
elif (data_set=="cifar"):
return(get_cifar())
The network
class MNIST_Net(nn.Module):
def __init__(self,pars):
super(MNIST_Net, self).__init__()
ks=pars.kernel_size
ps=np.int32(pars.pool_size)
self.mid_layer=pars.mid_layer
# Two successive convolutional layers.
# Two pooling layers that come after convolutional layers.
# Two dropout layers.
self.conv1 = nn.Conv2d(1, 32, kernel_size=ks[0],padding=ks[0]//2)
self.pool1=nn.MaxPool2d(kernel_size=[ps],stride=2)
self.conv2 = nn.Conv2d(32, 64, kernel_size=ks[1],padding=ks[1]//2)
self.drop2 = nn.Dropout2d(pars.dropout)
self.pool2=nn.MaxPool2d(kernel_size=2,stride=2)
self.drop_final=nn.Dropout(pars.dropout)
# Run the network one time on one dummy data point of the same
# dimension as the input images to get dimensions of fully connected
# layer that comes after second convolutional layers
self.first=True
if self.first:
self.forward(torch.zeros((1,)+pars.inp_dim))
# Setup the optimizer type and send it the parameters of the model
if pars.minimizer == 'Adam':
self.optimizer = torch.optim.Adam(self.parameters(), lr = pars.step_size)
else:
self.optimizer = torch.optim.SGD(self.parameters(), lr = pars.step_size)
self.criterion=nn.CrossEntropyLoss()
def forward(self, x):
# Apply relu to a pooled conv1 layer.
x = F.relu(self.pool1(self.conv1(x)))
if self.first:
print('conv1',x.shape)
# Apply relu to a pooled conv2 layer with a drop layer inbetween.
x = self.drop2(F.relu(self.pool2(self.conv2(x))))
if self.first:
print('conv2',x.shape)
if self.first:
self.first=False
self.inp=x.shape[1]*x.shape[2]*x.shape[3]
# Compute dimension of output of x and setup a fully connected layer with that input dim
# pars.mid_layer output dim. Then setup final 10 node output layer.
print('input dimension to fc1',self.inp)
if self.mid_layer is not None:
self.fc1 = nn.Linear(self.inp, self.mid_layer)
self.fc_final = nn.Linear(self.mid_layer, 10)
else:
self.fc1=nn.Identity()
self.fc_final = nn.Linear(self.inp, 10)
# Print out all network parameter shapes and compute total:
tot_pars=0
for k,p in self.named_parameters():
tot_pars+=p.numel()
print(k,p.shape)
# Calculate and print the number of parameters
print('tot_pars',tot_pars)
x = x.reshape(-1, self.inp)
x = F.relu(self.fc1(x))
x = self.drop_final(x)
x = self.fc_final(x)
return x
# Run the network on the data, compute the loss, compute the predictions and compute classification rate/
def get_acc_and_loss(self, data, targ):
output = self.forward(data)
loss = self.criterion(output, targ)
pred = torch.max(output,1)[1]
correct = torch.eq(pred,targ).sum()
return loss,correct
# Compute classification and loss and then do a gradient step on the loss.
def run_grad(self,data,targ):
loss, correct=self.get_acc_and_loss(data,targ)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return loss, correct
Run one epoch
def run_epoch(net,epoch,train,pars,num=None,ttype="train"):
if ttype=='train':
t1=time.time()
n=train[0].shape[0]
if (num is not None):
n=np.minimum(n,num)
ii=np.array(np.arange(0,n,1))
np.random.shuffle(ii)
tr=train[0][ii]
y=train[1][ii]
train_loss=0; train_correct=0
for j in trange(0,n,pars.batch_size):
# Transfer the batch from cpu to gpu (or do nothing if you're on a cpu)
data=torch.torch.from_numpy(tr[j:j+pars.batch_size]).to(pars.device)
targ=torch.torch.from_numpy(y[j:j+pars.batch_size]).type(torch.long).to(pars.device)
# Implement SGD step on batch
loss, correct = net.run_grad(data,targ)
train_loss += loss.item()
train_correct += correct.item()
train_loss /= len(y)
print('\nTraining set epoch {}: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(epoch,
train_loss, train_correct, len(y),
100. * train_correct / len(y)))
train_error_rate = 100. * (1 - train_correct / len(y))
#train_error_rates.append(train_error_rate)
return train_error_rate
def net_test(net,val,pars,ttype='val'):
net.eval()
with torch.no_grad():
test_loss = 0
test_correct = 0
vald=val[0]
yval=val[1]
for j in np.arange(0,len(yval),pars.batch_size):
data=torch.from_numpy(vald[j:j+pars.batch_size]).to(device)
targ = torch.from_numpy(yval[j:j+pars.batch_size]).type(torch.long).to(pars.device)
loss,correct=net.get_acc_and_loss(data,targ)
test_loss += loss.item()
test_correct += correct.item()
test_loss /= len(yval)
SSS='Validation'
if (ttype=='test'):
SSS='Test'
print('\n{} set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(SSS,
test_loss, test_correct, len(yval),
100. * test_correct / len(yval)))
test_error_rate = 100. * (1 - test_correct / len(yval))
#if ttype == 'val':
#test_error_rates.append(test_error_rate)
return test_error_rate
Run the training. Save the model and test at the end
import time
# An object containing the relevant parameters for running the experiment.
class par(object):
def __init__(self):
self.batch_size=1000
self.step_size=.001
# part a
self.num_epochs=20
self.numtrain=10000
self.minimizer="Adam"
self.data_set="mnist"
self.model_name="model"
self.dropout=0.
self.dim=32
self.pool_size=2
self.kernel_size=5
self.mid_layer=256
self.use_gpu=False
pars=par()
pars.__dict__
{'batch_size': 1000,
'step_size': 0.001,
'num_epochs': 20,
'numtrain': 10000,
'minimizer': 'Adam',
'data_set': 'mnist',
'model_name': 'model',
'dropout': 0.0,
'dim': 32,
'pool_size': 2,
'kernel_size': 5,
'mid_layer': 256,
'use_gpu': False}
# use GPU when possible
pars.device = device
pars.kernel_size=[5,5]
train,val,test=get_data(data_set=pars.data_set)
pars.inp_dim=train[0][0].shape
# Initialize the network
net = MNIST_Net(pars).to(pars.device)
# Post it to the gpu if its there.
net.to(pars.device)
(70000, 784) conv1 torch.Size([1, 32, 14, 14]) conv2 torch.Size([1, 64, 7, 7]) input dimension to fc1 3136 conv1.weight torch.Size([32, 1, 5, 5]) conv1.bias torch.Size([32]) conv2.weight torch.Size([64, 32, 5, 5]) conv2.bias torch.Size([64]) fc1.weight torch.Size([256, 3136]) fc1.bias torch.Size([256]) fc_final.weight torch.Size([10, 256]) fc_final.bias torch.Size([10]) tot_pars 857738 MNIST_Net( (conv1): Conv2d(1, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (pool1): MaxPool2d(kernel_size=[2], stride=2, padding=0, dilation=1, ceil_mode=False) (conv2): Conv2d(32, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (drop2): Dropout2d(p=0.0, inplace=False) (pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) (drop_final): Dropout(p=0.0, inplace=False) (fc1): Linear(in_features=3136, out_features=256, bias=True) (fc_final): Linear(in_features=256, out_features=10, bias=True) (criterion): CrossEntropyLoss() )
Total number of parameter: 857738, shown in the output below.
It is calculated by the following:
conv1.weight torch.Size([32, 1, 5, 5])
conv1.bias torch.Size([32])
-> 3215*5 + 32 = 832
conv2.weight torch.Size([64, 32, 5, 5])
conv2.bias torch.Size([64])
-> 64325*5 + 64 =51264
fc1.weight torch.Size([256, 3136])
fc1.bias torch.Size([256])
-> 25677*64 + 256 = 803072
fc_final.weight torch.Size([10, 256])
fc_final.bias torch.Size([10])
-> 10*256 + 10 =2570
-----> 832+51264+803072+2570 = 857738
# use GPU when possible
pars.device = device
pars.kernel_size=[5,5]
train,val,test=get_data(data_set=pars.data_set)
pars.inp_dim=train[0][0].shape
# Initialize the network
net = MNIST_Net(pars).to(pars.device)
# Post it to the gpu if its there.
net.to(pars.device)
train=(train[0][0:pars.numtrain],train[1][0:pars.numtrain])
# Initialize lists to store the training and validation error rates.
train_error_rates = []
test_error_rates = []
for i in range(pars.num_epochs):
# Run one epoch of training
train_error_rates.append(run_epoch(net, i, train, pars, num=pars.numtrain, ttype="train"))
# Test on validation set.
test_error_rates.append(net_test(net, val, pars))
original_train_error_rates = train_error_rates
original_test_error_rates = test_error_rates
# Save the model to a file
if not os.path.isdir(os.path.join(predir,'parta')):
os.mkdir(os.path.join(predir,'parta'))
torch.save(net.state_dict(), os.path.join(predir,'parta',pars.model_name))
(70000, 784)
conv1 torch.Size([1, 32, 14, 14])
conv2 torch.Size([1, 64, 7, 7])
input dimension to fc1 3136
conv1.weight torch.Size([32, 1, 5, 5])
conv1.bias torch.Size([32])
conv2.weight torch.Size([64, 32, 5, 5])
conv2.bias torch.Size([64])
fc1.weight torch.Size([256, 3136])
fc1.bias torch.Size([256])
fc_final.weight torch.Size([10, 256])
fc_final.bias torch.Size([10])
tot_pars 857738
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 0: Avg. loss: 0.0017, Accuracy: 5821/10000 (58.21%)
Validation set: Avg. loss: 0.0007, Accuracy: 4285/5000 (85.70%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 1: Avg. loss: 0.0006, Accuracy: 8271/10000 (82.71%)
Validation set: Avg. loss: 0.0003, Accuracy: 4543/5000 (90.86%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 2: Avg. loss: 0.0004, Accuracy: 8948/10000 (89.48%)
Validation set: Avg. loss: 0.0002, Accuracy: 4696/5000 (93.92%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 3: Avg. loss: 0.0003, Accuracy: 9222/10000 (92.22%)
Validation set: Avg. loss: 0.0002, Accuracy: 4744/5000 (94.88%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 4: Avg. loss: 0.0002, Accuracy: 9388/10000 (93.88%)
Validation set: Avg. loss: 0.0001, Accuracy: 4801/5000 (96.02%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 5: Avg. loss: 0.0002, Accuracy: 9494/10000 (94.94%)
Validation set: Avg. loss: 0.0001, Accuracy: 4827/5000 (96.54%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 6: Avg. loss: 0.0001, Accuracy: 9582/10000 (95.82%)
Validation set: Avg. loss: 0.0001, Accuracy: 4856/5000 (97.12%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 7: Avg. loss: 0.0001, Accuracy: 9646/10000 (96.46%)
Validation set: Avg. loss: 0.0001, Accuracy: 4883/5000 (97.66%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 8: Avg. loss: 0.0001, Accuracy: 9694/10000 (96.94%)
Validation set: Avg. loss: 0.0001, Accuracy: 4901/5000 (98.02%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 9: Avg. loss: 0.0001, Accuracy: 9716/10000 (97.16%)
Validation set: Avg. loss: 0.0001, Accuracy: 4907/5000 (98.14%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 10: Avg. loss: 0.0001, Accuracy: 9761/10000 (97.61%)
Validation set: Avg. loss: 0.0001, Accuracy: 4916/5000 (98.32%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 11: Avg. loss: 0.0001, Accuracy: 9776/10000 (97.76%)
Validation set: Avg. loss: 0.0001, Accuracy: 4907/5000 (98.14%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 12: Avg. loss: 0.0001, Accuracy: 9813/10000 (98.13%)
Validation set: Avg. loss: 0.0000, Accuracy: 4924/5000 (98.48%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 13: Avg. loss: 0.0001, Accuracy: 9822/10000 (98.22%)
Validation set: Avg. loss: 0.0001, Accuracy: 4925/5000 (98.50%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 14: Avg. loss: 0.0001, Accuracy: 9833/10000 (98.33%)
Validation set: Avg. loss: 0.0000, Accuracy: 4938/5000 (98.76%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 15: Avg. loss: 0.0000, Accuracy: 9862/10000 (98.62%)
Validation set: Avg. loss: 0.0000, Accuracy: 4939/5000 (98.78%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 16: Avg. loss: 0.0000, Accuracy: 9892/10000 (98.92%)
Validation set: Avg. loss: 0.0000, Accuracy: 4950/5000 (99.00%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 17: Avg. loss: 0.0000, Accuracy: 9900/10000 (99.00%)
Validation set: Avg. loss: 0.0000, Accuracy: 4945/5000 (98.90%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 18: Avg. loss: 0.0000, Accuracy: 9911/10000 (99.11%)
Validation set: Avg. loss: 0.0000, Accuracy: 4947/5000 (98.94%)
0%| | 0/10 [00:00<?, ?it/s]
Training set epoch 19: Avg. loss: 0.0000, Accuracy: 9918/10000 (99.18%)
Validation set: Avg. loss: 0.0000, Accuracy: 4939/5000 (98.78%)
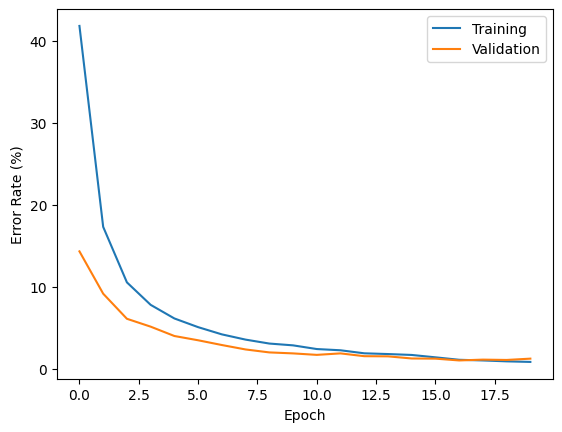
For each experiment, let's plot the error rate on training and validation as a function of the epoch number.
import matplotlib.pyplot as plt
plt.plot(range(pars.num_epochs), train_error_rates, label="Training")
plt.plot(range(pars.num_epochs), test_error_rates, label="Validation")
plt.xlabel("Epoch")
plt.ylabel("Error Rate (%)")
plt.legend()
plt.show()
Show an image with the 32 5×5 filters that are estimated in the first layer of the model.
filters = net.conv1.weight.detach().cpu().numpy()
fig, axes = plt.subplots(4, 8, figsize=(10, 5))
for i, ax in enumerate(axes.flatten()):
img = filters[i, 0, :, :]
ax.imshow(img, cmap="gray")
ax.axis("off")
plt.show()

Handling variability
A randomly shifted test set is been created in the function get mnist trans by taking each digit and applying random shift sampled uniformly between +/− shift/2 pixels in each direction.
import pylab as py
def get_mnist_trans(test_whole,shift):
test = test_whole[0]
ll=test.shape[0]
shift2=shift//2
uu=np.int32((np.random.rand(ll,2)-.5)*shift)
test_t=[]
for i,t in enumerate(test):
tt=np.zeros((28+shift+1,28+shift+1))
tt[shift2:shift2+28,shift2:shift2+28]=t
ttt=tt[shift2+uu[i,0]:shift2+uu[i,0]+28,shift2+uu[i,1]:shift2+uu[i,1]+28]
test_t.append(ttt.reshape(1,28,28))
test_trans_dat=np.float32(np.concatenate(test_t,axis=0).reshape((-1,1,28,28)))
print(test_trans_dat.shape)
return (test_trans_dat, test_whole[1])
For different sizes of shift, let's display a few of these examples alongside the original digits.
shift_list = [5, 10, 15]
num_examples = 10
fig, axes = plt.subplots(6, num_examples, figsize=(10, 9))
count = 0
for shift in shift_list:
test_trans_dat, test_trans_labels = get_mnist_trans(val, shift)
for i in range(num_examples):
axes[count, i].imshow(val[0][i, 0])
axes[count, 0].set_title('original')
axes[count, i].axis('off')
axes[count + 1, i].imshow(test_trans_dat[i, 0])
axes[count + 1, 0].set_title('after shift = ' + str(shift))
axes[count + 1, i].axis('off')
count = count + 2
plt.show()
(5000, 1, 28, 28)
(5000, 1, 28, 28)
(5000, 1, 28, 28)

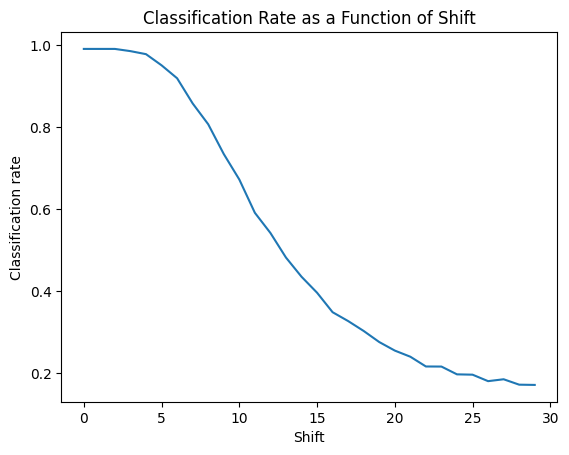
Using the original trained network to test on this data set. Let's show the classification rate as a function of shift.
trained_net = MNIST_Net_Triple(pars).to(pars.device)
trained_net.load_state_dict(torch.load(os.path.join(predir,'partb_full',pars.model_name)))
trained_net.to(pars.device)
shift_classification_rates = []
error_rates = []
shift_range = range(30)
for shift in shift_range:
val_trans_dat, val_trans_labels = get_mnist_trans(val, shift)
val_trans = (val_trans_dat, val_trans_labels)
error_rate = net_test(trained_net, val_trans, pars)
shift_classification_rates.append(1 - error_rate / 100)
error_rates.append(error_rate / 100)
plt.plot(shift_classification_rates)
plt.title("Classification Rate as a Function of Shift")
plt.xlabel("Shift")
plt.ylabel("Classification rate")
plt.figure()
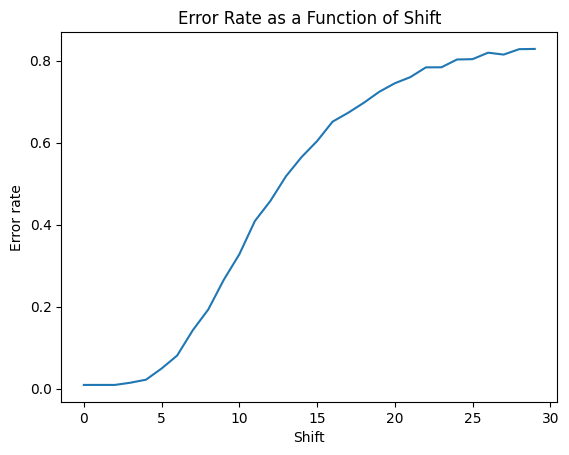
plt.plot(error_rates)
plt.title("Error Rate as a Function of Shift")
plt.xlabel("Shift")
plt.ylabel("Error rate")
conv1 torch.Size([1, 96, 14, 14])
conv2 torch.Size([1, 192, 7, 7])
input dimension to fc1 9408
conv1.weight torch.Size([96, 1, 5, 5])
conv1.bias torch.Size([96])
conv2.weight torch.Size([192, 96, 5, 5])
conv2.bias torch.Size([192])
fc1.weight torch.Size([256, 9408])
fc1.bias torch.Size([256])
fc_final.weight torch.Size([10, 256])
fc_final.bias torch.Size([10])
tot_pars 2874762
conv1.weight torch.Size([96, 1, 5, 5])
conv1.bias torch.Size([96])
conv2.weight torch.Size([192, 96, 5, 5])
conv2.bias torch.Size([192])
fc1.weight torch.Size([256, 9408])
fc1.bias torch.Size([256])
fc_final.weight torch.Size([10, 256])
fc_final.bias torch.Size([10])
tot_pars 2874762
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0000, Accuracy: 4955/5000 (99.10%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0000, Accuracy: 4955/5000 (99.10%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0000, Accuracy: 4955/5000 (99.10%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0001, Accuracy: 4928/5000 (98.56%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0001, Accuracy: 4891/5000 (97.82%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0002, Accuracy: 4755/5000 (95.10%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0004, Accuracy: 4597/5000 (91.94%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0008, Accuracy: 4290/5000 (85.80%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0011, Accuracy: 4036/5000 (80.72%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0018, Accuracy: 3673/5000 (73.46%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0026, Accuracy: 3362/5000 (67.24%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0033, Accuracy: 2956/5000 (59.12%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0040, Accuracy: 2710/5000 (54.20%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0049, Accuracy: 2410/5000 (48.20%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0057, Accuracy: 2176/5000 (43.52%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0064, Accuracy: 1981/5000 (39.62%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0072, Accuracy: 1743/5000 (34.86%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0076, Accuracy: 1635/5000 (32.70%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0082, Accuracy: 1514/5000 (30.28%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0086, Accuracy: 1379/5000 (27.58%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0090, Accuracy: 1275/5000 (25.50%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0091, Accuracy: 1200/5000 (24.00%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0095, Accuracy: 1081/5000 (21.62%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0095, Accuracy: 1080/5000 (21.60%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0096, Accuracy: 985/5000 (19.70%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0096, Accuracy: 981/5000 (19.62%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0097, Accuracy: 902/5000 (18.04%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0095, Accuracy: 925/5000 (18.50%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0096, Accuracy: 859/5000 (17.18%)
(5000, 1, 28, 28)
Validation set: Avg. loss: 0.0093, Accuracy: 856/5000 (17.12%)
Text(0, 0.5, 'Error rate')